变分自编码器（VAE）的本质：使用神经网络实现变分推断的计算

甲方的增量需求，以及神经网络上的约束条件，都可以转化成损失函数的惩罚项。———— 沃·兹基硕德

变分自编码器是一种经典的深度生成模型，在图像生成、协同过滤等任务上有着重要的应用，有着举足轻重的历史地位。

回顾：变分推断的本质

书接上文。在变分推断的介绍中，我们已经明确了变分推断方法的本质：用一个简单分布拟合另一个复杂分布。并且我们已知，变分推断包含一下几个步骤：

1. 给定观测数据，计算隐变量Z的简单分布. 其中为分布族的参数，例如正态分布中的均值和方差；二项分布中的正面概率.
2. 根据观测数据，计算证据下界.
3. 优化简单分布族的参数，使得证据下界最大化. 这一步蕴含两个要素：
   1. 最大化观测变量的拟合值（最优重建）
   2. 使隐变量估计简单分布与其先验分布尽可能地接近

正题：变分自编码器的本质

变分自编码器的本质在于，使用神经网络建模隐变量的简单分布 和观测变量的后验概率 ，使用反向传播方法完成证据下界最大化的参数优化过程。

我们首先给出变分自编码器的结构图，然后介绍它具体的工作原理。

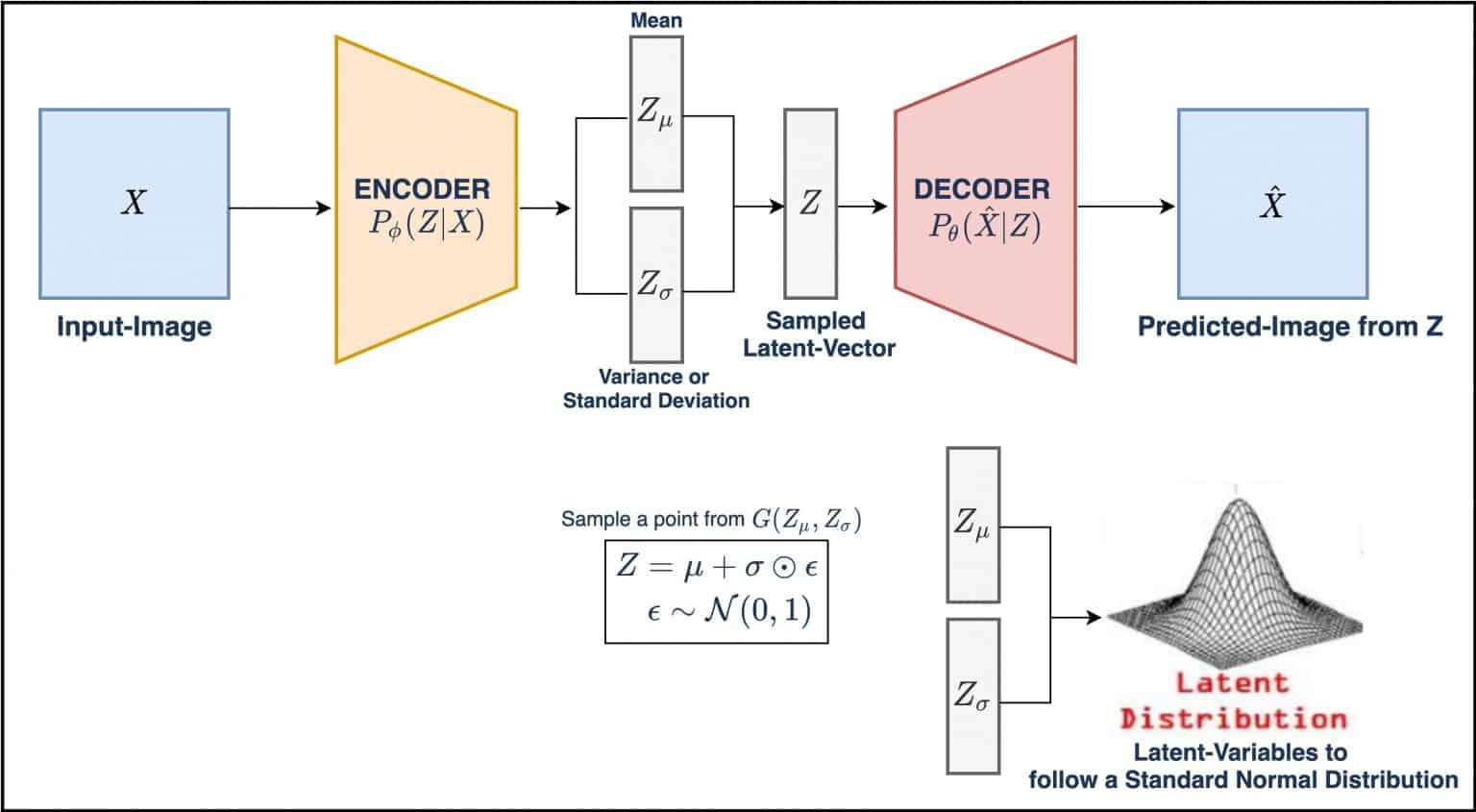
变分自编码器的工作流程

变分自编码器的工作流程如下：

1. 输入观测数据，使用基于神经网络的Encoder计算隐变量的分布参数（注意，计算结果不是隐变量本身，因为变分推断中隐变量是随机变量，需要从分布中采样得到）
2. 使用重参数化技巧采样得到隐变量（例如上图中的得到隐变量）.重参数化技巧的内涵在于将随机变量的随机性与其分布特征解耦，从而能够实现后者的反向传播优化.
3. 输入隐变量，使用基于神经网络的Decoder计算重建的观测数据
4. 计算损失函数（即证据下界，），使用反向传播方法优化Encoder和Decoder.

ELBO的本质：带惩罚项的损失函数

在上文中，我们已经说明了，证据下界的定义如下：

$$ELBO(q)=E_Z[\log p(X|Z)]-KL(q_\phi(Z)||p(Z))$$

本质上，等式右侧的第一项，是用于最优化重建观测变量的损失函数主项，可以用交叉熵、均方根误差等常见的神经网络损失函数代替；第二项是用于使隐变量的后验分布参数尽可能接近先验分布 的惩罚项，例如先验分布为，则该项使得Encoder生成的的期望尽可能接近0，方差尽可能接近1. 一个经典的ELBO的实现如下：

$$L(\Omega)=CrossEntropy(X,\hat{X})−1/2(log\sigma_\phi^2−\sigma_\phi^2−\mu_\phi^2+1)$$

其中是变分自编码器的所有可优化参数，和分别是隐变量的期望和方差. 该损失函数适用于标准正态先验分布.

另一个适用于标准二项先验分布的ELBO实现如下：

$$L(\Omega)=CrossEntropy(X,\hat{X})−(p_\phi\log p_\phi + (1-p_\phi)\log(1-p_\phi))$$

其中是由Encoder计算的的概率. 服从二项分布.

参考文献

[1] JKRD.变分推断的本质

[2] David M. Blei, Alp Kucukelbir, & Jon D. McAuliffe (2016). Variational Inference: A Review for Statisticians. CoRR, abs/1601.00670.

[3] DOERSCH C. Tutorial on Variational Autoencoders[J]. stat, 2016, 1050: 13.